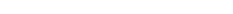Examine the graphs of measurements carefully. Each point represents a person. The point’s horizontal position on the graph (X axis) is based on a person’s foot length or stride length measurements, while the point’s position on the vertical axis (Y axis) is based on the person’s height measurement. Note that the points are not scattered in all parts of the graph like the stars in the night sky. Instead, the points cluster roughly along an invisible line that runs from the lower left to the upper right corners of the graph. You can use this clustering pattern as a way to identify and evaluate trends in these data which can then be used to predict the height of the Laetoli hominins that lived 3.7 million years ago.
Regression:
Do you see a trend in these data that reveals a relationship between foot length and body height, and/or stride length and body height? Individuals with long strides and long feet are taller than those individuals with short feet and short strides, so points on the right-hand side of the graph also tend to be closer to the top of the graph.
Take a look at the straight line that is centered both vertically and horizontally within the cloud of data points. This trend line, called a regression line, permits you to estimate the average height for an individual based on a given foot length or stride length. You can do this by picking some value for X (or a value on the horizontal axis) and follow this value vertically (up) until it intersects with the regression line. Then, follow this point horizontally to the y-axis on the left where you can read the height value.
Correlation:
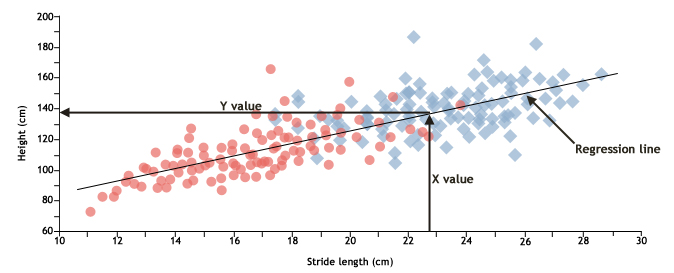
A relationship between two variables, such as X and Y, is called a correlation. We can summarize the correlation between two variables by calculating the correlation coefficient (r) which is the degree of covariance between the two variables. The correlation coefficient will always fall between -1 and 1. A negative correlation mean that as the value for X gets bigger, the value of Y tends to get smaller. A positive correlation means that as the value for X gets bigger, the value of Y tends to get bigger as well. The closer r is to 1 or -1, the more dependent the relationship between X and Y.
In the graphs below, the purple line represents increasing values, and the green line represents decreasing values. In the first graph, depicting a positive correlation, the value of Y increases as the value of X increases. The second graph depicts a negative correlation, where the green arrow indicates that values for Y decrease as the values for X increases.
Prediction:
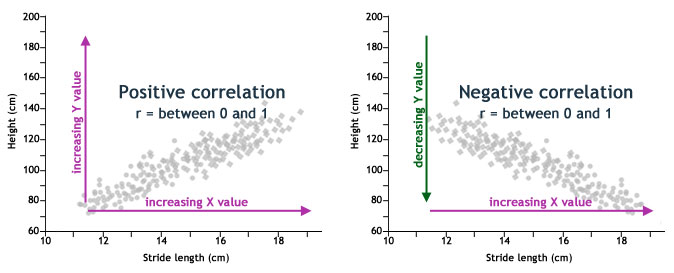
Regression is related to correlation, but regression is a type of statistical analysis that lets you predict a value of Y based on the value of X. We can calculate several parameters about the regression line including the slope (m), and the coefficient of determination (R2).
Examine the values for the trackways data shown in the graph below. The slope, or m, of the regresion line tells you how much change in X you can expect based on a given change in Y. R2 tells you how much of the variation in Y is attributable to variation in X. For instance, if your R2 = 0.9, you can say that 0.9 or 90% of the variation in Y is due to the variation in X. The rest of the variation, or “noise”, is accounted by other factors, such as measurement error, individual variation, etc.
To see an example of how a regression line is calculated, watch this regression line example video on the Khan Academy website.
Evaluation:
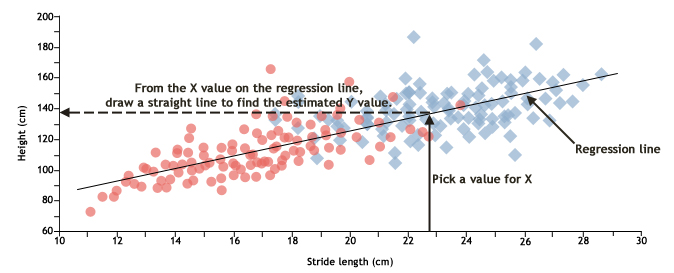
In this lab, we have provided the correlation coefficient and the regression line for the relationship between foot length and stride length compared with body height. Remember, not all correlations represent a close relationship between variables. Returning to the Trackways graphs, you will see that the data plotted on one graph seem more tightly clustered around the regression line than the data plotted on the second graph. The more tightly clustered a dataset, the more dependent the variables are upon one another. Thus, we can hypothesize about which correlation, foot length and body height or stride length and body height, provides a more accurate prediction for body height based on how the data are clustered around the regression line.
To estimate the height of the Laetoli hominins, you will first plot the X value for the Laetoli hominins (either foot length or stride length). Next, use the regression line to determine the corresponding Y value (height) of the individuals who made the 3.7 Ma tracks at Laetoli. You can then determine the most likely height of the hominins by evaluating which correlation is the most likely to provide you with an accurate result: foot length and body height, or stride length and body height.